¿Por qué las papas fritas tienen forma curva? Hay matemáticas detrás
La forma de las papas fritas, con un diseño innovador, está basada en un paraboloide hiperbólico y es un ejemplo claro de geometría aplicada a la ingeniería de alimentos.
- Científicos detectan que el núcleo de la Tierra parece estar rodeado de múltiples capas: un hallazgo que cambiaría nuestra comprensión del planeta
- Científicos curan el cáncer de páncreas en ratones: ¿podría llegar a probarse el tratamiento en humanos?
En el mundo de los snacks, pocos productos han despertado tanta curiosidad matemática como la curvatura de los snacks de papas fritas. Detrás de su forma en “silla de montar” hay más que una decisión estética o de marketing: se trata de una estructura diseñada con precisión científica. Este diseño, creado en 1956 por el científico y químico Frederic Baur, fue producto de cálculos complejos apoyados por supercomputadoras, y sigue siendo uno de los casos más populares de geometría aplicada en la industria alimentaria.
En concreto, la forma de estos chips responde al concepto geométrico del paraboloide hiperbólico, una superficie con doble curvatura que ha demostrado ser clave tanto para su resistencia como para su fácil almacenamiento y transporte. Esta geometría, lejos de ser decorativa, cumple una función estructural y funcional en el producto.
¿Por qué los ingenieros diseñaron las papas con esta forma?
El diseño no fue accidental ni estético. Las primeras versiones del snack sufrían frecuentes roturas durante el empaque y distribución. Para resolver este problema, Baur, junto a un equipo de ingenieros, ideó una forma que otorgara resistencia estructural sin aumentar el grosor del chip.
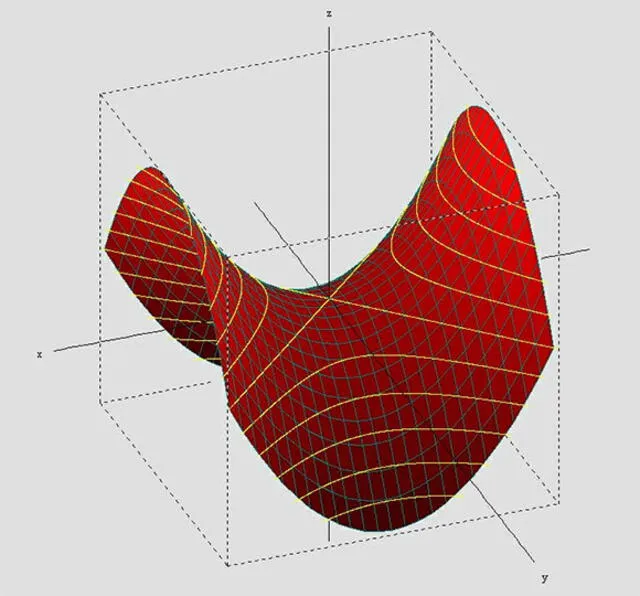
Un paraboloide hiperbólico es una superficie geométrica que recuerda a la silla de montar de un caballo, y la patata frita tiene la forma de un segmento de ella. Foto: Wikimedia
La forma en paraboloide hiperbólico permite que las papas se apilen perfectamente, distribuyendo el peso sin generar puntos de presión que las fracturen. Estudios indicaron que una sola papa puede soportar hasta 150 gramos de peso sin romperse. Además, este diseño reduce el movimiento del chip en la línea de producción, facilitando el envasado sin pérdidas.
También influye en la experiencia del consumidor: al quebrarse, el chip genera fragmentos irregulares, lo que intensifica la sensación de crocancia. Esta característica sensorial se pensó como un valor añadido dentro del proceso de ingeniería de alimentos.
Las papas en matemáticas
La estructura que caracteriza a las papas fritas curvas se llama paraboloide hiperbólico, una figura tridimensional reconocida por su curvatura en dos direcciones opuestas. En términos matemáticos, su ecuación se expresa como:
z = (y² / b) - (x² / a), donde “a” y “b” son constantes positivas. Esta fórmula permite generar una superficie que presenta una forma cóncava en un eje y convexa en otro, produciendo así el famoso perfil en forma de silla.
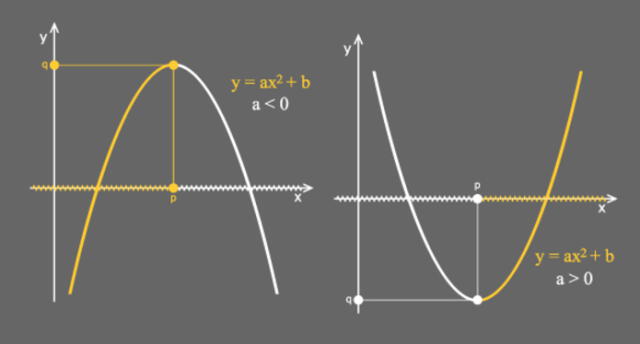
Dos parábolas de direcciones opuestas se esconden en la superficie de un paraboloide hiperbólico. Foto: Shutterstock
Además, esta superficie es una superficie reglada, es decir, en ella se pueden trazar líneas rectas que se apoyan completamente sobre la curvatura del objeto. Esta propiedad es lo que permite que un chip tan delgado pueda, sorprendentemente, pasar por aberturas estrechas sin romperse, como lo demostró la divulgadora científica Kyle Hill en una prueba viral.
¿Qué otros usos tiene esta forma matemática?
El paraboloide hiperbólico no solo vive en las papas fritas curvas. Este diseño ha sido ampliamente utilizado en arquitectura y matemáticas aplicadas. Su capacidad para distribuir cargas lo convierte en una forma ideal para techos de grandes estructuras.
Entre los ejemplos más conocidos están el London Velodrome en Reino Unido, el Scotiabank Saddledome en Canadá y el estadio Scandinavium en Suecia. Todos ellos utilizan esta forma para ganar en resistencia estructural sin necesidad de materiales adicionales.
Incluso en objetos cotidianos como una cinta de Möbius —otra superficie reglada— se puede ver cómo la matemática se cuela en nuestro día a día. Así, lo que parece una simple papa frita, en realidad es un resumen comestible de siglos de desarrollo científico.
