¿Qué es el diámetro, cuáles son sus características y cómo calcularlo?
Revisa aquí qué es el diámetro y por qué es tan importante conocerlo. Además, repasa algunas de las operaciones que podremos efectuar para hallarlo.
Saber qué es el diámetro de una circunferencia es importante para muchos ámbitos de la vida cotidiana donde estas figuras son protagonistas. Valores como el área de un círculo se vuelven bastante fáciles de determinar cuando tenemos esta cifra.
En ese sentido, es necesario repasar las distintas operaciones geométricas que involucran al diámetro. Conoce aquí qué es esta cifra y cómo calcularla, así como los usos que tiene el conocerla y las propiedades que posee.
¿Qué es el diámetro?
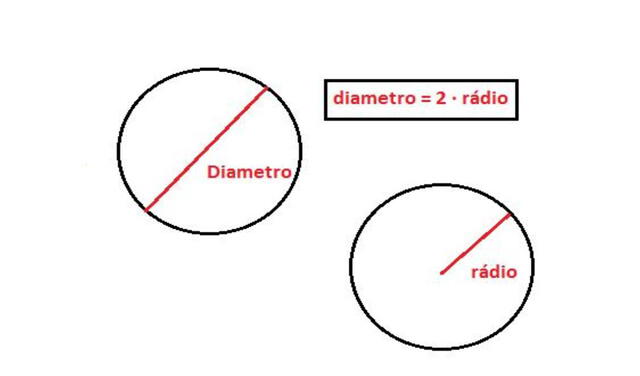
El diámetro se define como un segmento de recta que une dos puntos opuestos de una circunferencia y pasa por el centro de esta. Mide el doble del radio del círculo y divide a este en dos semicírculos perfectos.
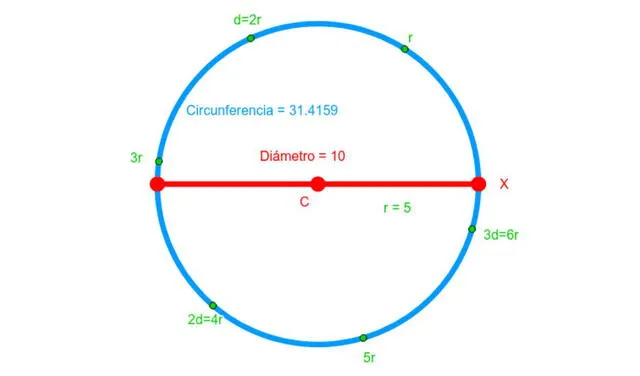
Diámetro de una circunferencia. Foto: Geogebra
¿Cómo se mide un diámetro?
Si se conoce el radio del círculo
Multiplica el radio por 2, ya que el diámetro equivale al doble de dicha longitud.
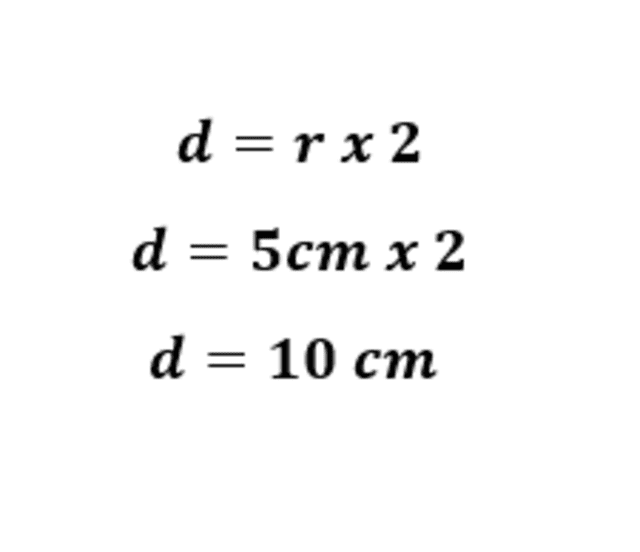
Fórmula para hallar el diámetro de una circunferencia. Foto: Tecno How To
Si se conoce la circunferencia del círculo
Divide el valor de la circunferencia entre pi (π), cuyo valor aproximado es de 3,1416.
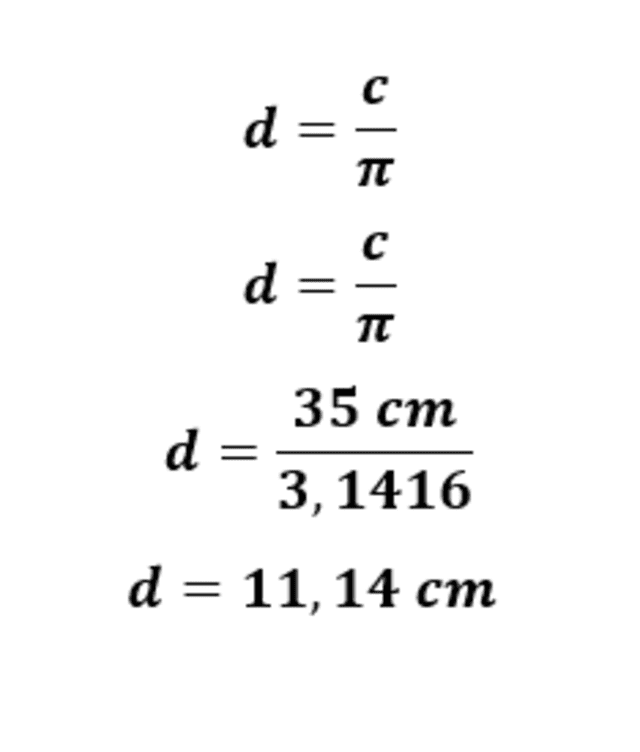
Fórmula para hallar el diámetro de una circunferencia. Foto: Tecno How To
Si se conoce el área del círculo
Se divide el valor del área entre pi (π) y se le saca la raíz cuadrada al resultado.
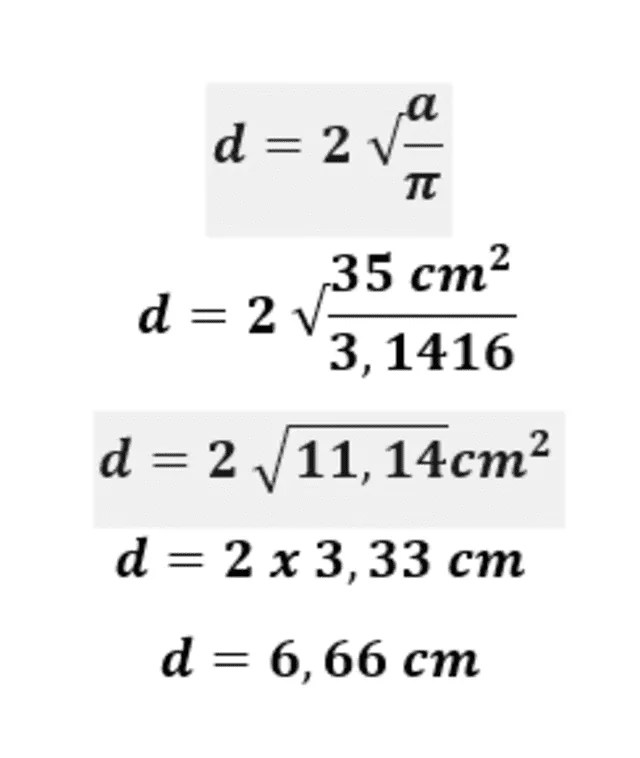
Fórmula para hallar el diámetro de una circunferencia. Foto: Tecno How To
¿Cómo sacar el área de un círculo con el diámetro?
- Primero, se divide el valor de pi entre 4. Si se toma pi como 3,14, el resultado será aproximadamente 0,785.
Fórmula para sacar el área del círculo con el diámetro. Foto: Un Como
- Luego, saca el cuadrado del valor del diámetro y multiplica el resultado por el cuarto de pi.
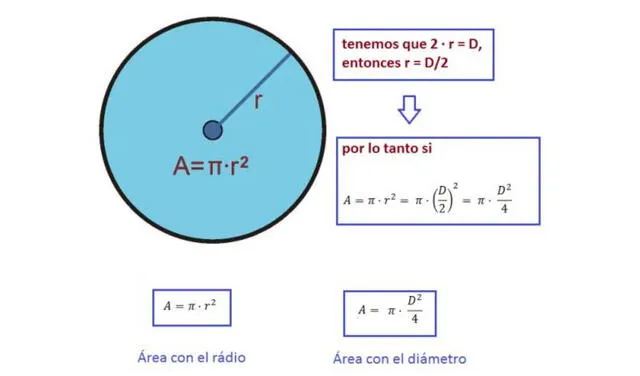
Fórmula para sacar el área del círculo con el diámetro. Foto: Un Como
Propiedades del diámetro
- El diámetro de una circunferencia mide el doble de su radio.
- El diámetro divide a la circunferencia en dos semicircunferencias con la misma longitud.
- El diámetro divide al círculo en dos figuras o semicírculos con la misma superficie.
- Todo diámetro de una circunferencia perpendicular a una cuerda divide a ésta en dos partes iguales.
- Cualquier triángulo formado con un diámetro será rectángulo, es decir, tendrá un ángulo de 90°.
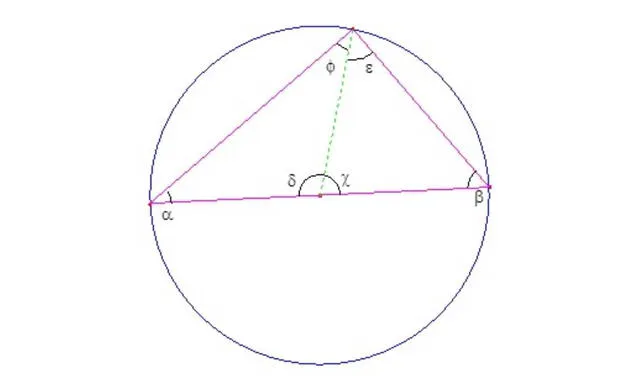
Triángulo rectángulo que se forma con el diámetro. Foto: Universidad Santo Tomás
Usos del diámetro
Conocer el diámetro de una circunferencia puede ser muy útil en campos donde se trabajen con figuras planas, tales como:
- Ingeniería
- Electricidad
- Electrónica
- Mecánica
- Arquitectura
- Navegadores, entre otros.
Ejemplos de problemas con diámetro
Si el diámetro de la Tierra es de 12.756 kilómetros, ¿cuál es la medida de su circunferencia?
Solución: El valor de la circunferencia se puede obtener multiplicando el diámetro por pi. En este caso, multiplicamos:
- C = (π) d = (3,14) 12.756 = 40.053,84 kilómetros
Si una glorieta tiene una circunferencia que mide 70 metros, ¿cuánto mide su diámetro?
Solución: Dividimos el valor de la circunferencia entre el valor aproximado de pi.
- d = C / π = 70 / 3,14 = 22,29 metros.
Encuentra el área de un círculo de diámetro 16.
Solución: Sacamos el cuadrado del diámetro y lo multiplicamos por el cuarto de pi.
- A = 16 2 (π /4) = 256 (0,785) = 0,785
