¿Cuáles son los número primos y cómo se calculan?
Conoce AQUÍ todo sobre los números primos: su definición, para qué sirven y cómo se calculan.
Los números primos son componentes imprescindibles de las matemáticas. Gracias a ellos podemos formular algoritmos y cálculos que nos permiten resolver todo tipo de problemas del día a día. Además, conocerlos a fondo nos ayudará a comprender de mejor manera el mundo donde vivimos. Por eso, en esta nota, te enseñaremos todo sobre los números primos, desde su definición hasta cómo calcularlos.
¿Qué son los números primos?
Los números primos son aquellos números naturales que solamente se pueden dividir por sí mismos y por 1, es decir, que si intentamos dividirlos por cualquier otro número, el resultado no es entero. Por ejemplo, el 7 es un número primo porque solo es divisible por 7 y por 1.
TE RECOMENDAMOS
ELECCIONES Y CONTINÚA PERSECUCIÓN PARLAMENTARIA |SIN GUION CON ROSA MARÍA PALACIOS
Cabe resaltar que, el número 1 solo tiene un divisor, que es sí mismo, por eso no es considerado como un número primo.
¿Cuáles son los números primos del 1 al 100?
El primer número primo es el 2, y en total existen 25 números primos entre 1 y 100. Los cuales son:
- Números primos del 1 al 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
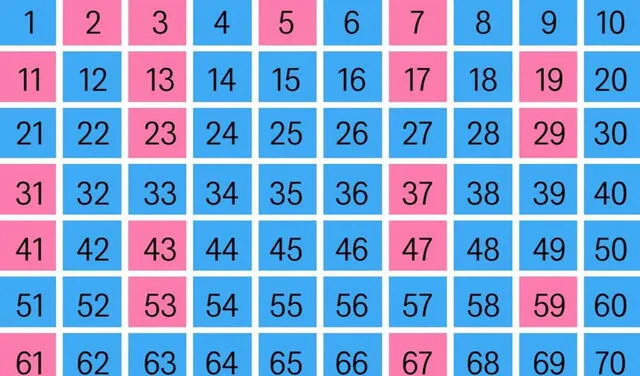
Números primos (en rojo) del 1 al 70. Foto: 20 Minutos
¿Cómo saber si un número es primo?
Para poder demostrar si un número es primo o no, solo tienes que dividir ordenadamente el número en cuestión por todos los números primos menores que él (2, 3, 5, 7, 11, entre otros). Si al realizar las divisiones, no se obtiene un resultado exacto y el cociente es menor o igual al divisor, podremos afirmar que el número analizado es primo.
Ejemplo: Determinar si 113 es un número primo.
- 113 no es divisible por 2 (divisor: 2, cociente: 56.5)
- 113 no es divisible por 3 (divisor: 3, cociente: 37.6)
- 113 no es divisible por 5 (divisor: 5, cociente: 22.6)
- 113 no es divisible por 7 (divisor: 7, cociente: 16.1)
- 113 no es divisible por 11 (divisor: 11, cociente: 10.2)
En el último resultado, podemos notar que el cociente es menor que el divisor, entonces es momento de detenernos para analizar si alguno de los resultados es un número entero. Como ninguno lo es, podemos decir que 113 es un número primo.
¿Para que sirven los números primos?
Los número primos sirven para asentar las bases de cualquier número, ya que son imprescindibles en el Teorema Fundamental de la Aritmética, que plantea que para cualquier número del uno al infinito existe una descomposición de números primos única.
Además, sin ellos no podemos elaborar algoritmos y cálculos complejos. Actualmente, las matemáticas son la base de nuestro conocimiento técnico/científico. Sin los números primos no se podría hacer nada de lo que hacemos y un ejemplo de ello es su uso en la criptografía. Una aplicación que ayuda a mantener seguras las transacciones en Internet y demás operaciones informáticas.
¿Cómo encontrar los números primos con la criba de Eratóstenes?
El matemático griego Eratóstenes ideó una manera rápida de obtener todos los números primos hasta uno concreto. Se trata de un método denominado criba de Eratóstenes.
Se basa en eliminar de la lista de números todos los que sean compuestos. Una vez acabado el proceso, los números que queden sin descartar serán primos. La criba de Eratóstenes se para en el momento en que el cuadrado del número a investigar es mayor que el último número de la lista (casi siempre es menor que 100).
